Graph Theory:
In this post, I would briefly go over through how and what led to the development of the graph theory which revolutionized the way many complicated problems were
looked at and were solved.
Problem
The ‘Königsberg
bridge’ problem originated in the city of Königsberg, formerly in Germany but, now known as Kaliningrad and part of Russia, located on the river Preger. The city had seven bridges, which connected two islands with the main-land
via
seven bridges. People staying there always wondered
whether was there any way
to walk over
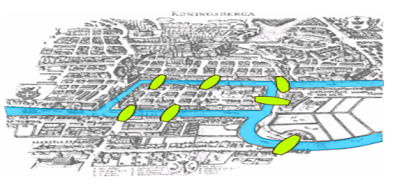
all the bridges once and only once. The below picture is the map of Königsberg
during Euler's time showing the actual layout of the seven bridges, highlighting the river Preger and the bridges.
Fig. 1
Fig. 2
This simplifies
the
problem to great extent. Now, the problem can be merely seen as the
way
of tracing the graph with a pencil without actually lifting it. One can try it in all
possible ways, but you will soon figure out, it is not possible. Euler proposed that any given graph can be traversed with
each edge traversed exactly once if and only if it had, zero or exactly two nodes with odd degrees. The graph following this condition is called, Eulerian circuit or path.
In actual case of seven bridges of Königsberg, once the situation was presented in terms of graph, the case was simplified as the graph had just 4 nodes, with each node having odd degree. So, Euler concluded that these bridges cannot be traversed exactly once.
Using this theorem, we can create
and
solve number of problems. Suppose now, we want to make the graph created from bridges of Königsberg, a Euler’s circuit. Now, as per
Euler’s theorem we need to introduce a path to make the degree of two nodes even. And other two nodes can be of odd degree out of which one has to be starting and other another the endpoint. Suppose we want to start our journey from blue node and end at the
yellow node. So, the two nodes can have odd edges. But somehow we need to edit the actual graph by adding another edge to the graph such that the two other nodes have even
degree. So, the resulting figure is shown below.
Fig. 3


No comments:
Post a Comment